2025--ACM&TC第三次招新赛题解

题目难度：

签到：9、12

简单：2、5、8、11

中等：3、4、7

困难：1、6、10

题解

1、中位数

题目给出的n为奇数，那么最终的中位数一定是中间的那个数，于是我们可以二分答案，不断地去枚举答案

#include <bits/stdc++.h>
using namespace std;
#define int long long

int a[200005];
int n, k;

bool check(int x) {
    int sum = 0;
    int m = (n + 1) / 2; 
    for (int i = m; i <= n; i++) {
        if (a[i] < x) {
            sum += x - a[i];  
            if (sum > k) return 1; 
        }
    }
    return sum > k;  
}

signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);

    cin >> n >> k;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    sort(a + 1, a + 1 + n); 

    int l = a[(n + 1) / 2], r = 1e18;  
    while (l + 1 < r) {
        int mid = (l + r) / 2;
        if (check(mid)) {
            r = mid; 
        } else {
            l = mid; 
        }
    }
    cout << l << '\n';  

}

2、怕挂科的George

这题考的就是结构体的排序，也是看看一些人补没补题，如果第一场招新赛的第 4 题没写出来但补了的话，这一题也是肯定能写出来的。然后就是平均数记得开float或者double，感觉会有很多人开int然后WA好多发（学长赛前预测），学长出题的时候专门手搓了几个卡 int 的数据，嘿嘿~。

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"

struct stus{
    int s,a;
}stu[105];

bool cmp(stus c,stus d){
    return c.s<d.s;
}

int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
    int n,m;
    cin>>n>>m;
    double sum=0;
    for(int i=1;i<=n;++i){
        cin>>stu[i].s>>stu[i].a;
        sum+=stu[i].a;
        if(stu[i].s==m&&stu[i].a<60)
            stu[i].a=60;
    }
    double avg=sum/n;
    for(int i=1;i<=n;++i){
        if(stu[i].s!=m&&stu[i].a>=avg){
            stu[i].a=max(stu[i].a-2,0);
        }
    }
    sort(stu+1,stu+n+1,cmp);
    for(int i=1;i<=n;++i){
        cout<<stu[i].a<<" ";
    }
    cout<<endl;
    return 0;
}

3、位运算终于来了

这道题你首先要清楚 异或运算是什么，当前位相同为0，不同为1，这样根据这个规律我们可以在a的当前位与b的当前位不同时让a去异或2的当前位次幂(1,10,100,1000....)，比如a：(1001), b: (110),当枚举到第1位（从后往前）a为0，b为1那需要让a异或2的1次方，可以让a的当前位变为1，这样你会发现当到达当前位枚举过的位都是相同的，如果枚举到2的k次方大于a，那么不可能让a最终等于b，当然还有别的做法

#include <bits/stdc++.h>
using namespace std;
#define int long long

int ksm(int a, int b){
    int ans = 1;
    while(b){
        if(b % 2){
            ans = ans * a;
        }
        b = b / 2;
        a = a * a;
    }
    return ans;
}
void solve(){
    int a, b;
    cin >> a >> b;
    if(a == b){
        cout << 0 << '\n';
        return;
    }
    int aa = a;
    vector<int> ans;
    string s;
    for(int i = 0;; i++){
        if (a == 0 && b == 0) break;
        int x = ksm(2, i);
        if((a & 1) != (b & 1)){
            ans.push_back(x);
            if(x > aa){
            cout << -1 << '\n';
            return;
        }
        }
        a = a >> 1;
        b = b >> 1;
    }
    cout << ans.size() << '\n';
    for(auto t : ans){
        cout << t << ' ';
    }
    cout << '\n';
}
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);

    int t;
    cin >> t;
    while(t--){
        solve();
    }
}

4、我要打瓦！颗秒！！棒棒棒棒！！！

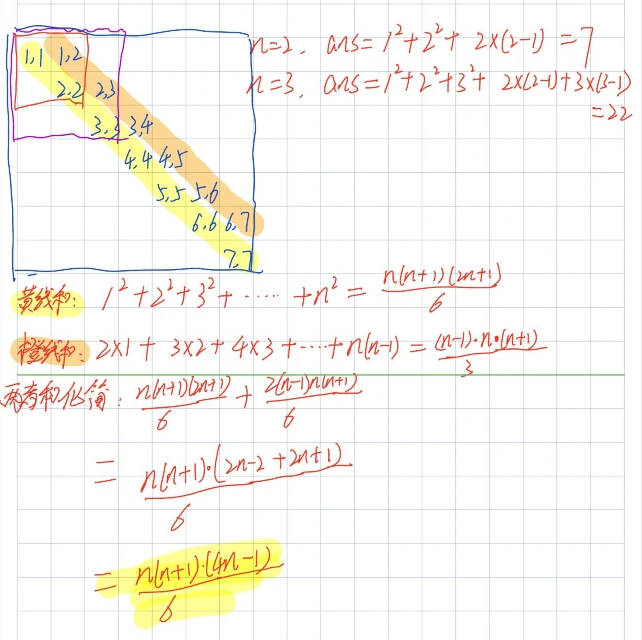
这题考的就是你们高中学的n的平方的前n项和通项公式（不知道你们老师有没有让背过，大部分老师应该都让背过）。不要觉得这题很奇怪，数学在计算机及 ACM 中很重要，说白了对于 ACM 来说编程语言只是工具，解题思路大部分都是靠数学思维，包括你们学的高数，和以后学的线代、离散、概率论等都会是 ACM 的考点（我记得去年招新赛，我们学长给我们出了一道二项式定理，感兴趣的自己可以看一下），计算机和数学相关性很大的，比如数学中的离散和计算机中的数据结构重合度很高，内容大部分都一样。这题的题解废话有点多了，主要也是想要让你们了解一下数学和计算机的关系，下面是正式题解：

随便举几个例子画画图就能知道移动的路线尽可能往中间靠才能让 ans 最大化，所以使 ans 最大化的路线就是先向右再向下，这样一直循环到 (n,n) 。通过下面两个重要的数学公式，可以推导出答案为：n * (n + 1) * (4 * n - 1) / 6。需要注意此题除法放在最后，避免前面没除尽，出现小数造成误差，模数 2022 最后可以和分母 6 约分成 337 ；还有就是边运算边取模，因为计算过程中会超出 long long 的范围 1e18 ；以及n也需要开long long ，因为n参与下面ans的计算了。具体计算过程见下图，黄线和就是n的平方的前n项和通项公式，橙线和则可以拆成等差数列的前n项和通项公式与n的平方的前n项和通项公式的和。

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"

const int mod=1e9+7;

int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        long long n;
        cin>>n;
        long long ans=337*n%mod*(n+1)%mod*(4*n-1)%mod;
        cout<<ans<<endl;
    }
    return 0;
}

5、带派不老铁?

起始位置由 ( 0 , 0 ) 到 ( x , y ) ，其结果只有三种情况。
1.输出结果为-1：当x=y或x=y+1或y=1时，此时一定不满足题目要求，输出-1；
2.输出结果为2：满足y>x即可
3.输出结果为3：剩下的情况都是3步

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"

int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        int x,y;
        cin>>x>>y;
        if(x==y||x==y+1||y==1)
            cout<<-1<<endl;
        else if(x<y)
            cout<<2<<endl;
        else
            cout<<3<<endl;
    }
    return 0;
}

//
// ⠀⠀⠀             ⠀⢸⣿⣿⣿⠀⣼⣿⣿⣦⡀
// ⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⠀⠀⠀ ⠀⢸⣿⣿⡟⢰⣿⣿⣿⠟⠁
// ⠀⠀⠀⠀⠀⠀⠀⢰⣿⠿⢿⣦⣀⠀⠘⠛⠛⠃⠸⠿⠟⣫⣴⣶⣾⡆
// ⠀⠀⠀⠀⠀⠀⠀⠸⣿⡀⠀⠉⢿⣦⡀⠀⠀⠀⠀⠀⠀ ⠛⠿⠿⣿⠃
// ⠀⠀⠀⠀⠀⠀⠀⠀⠙⢿⣦⠀⠀⠹⣿⣶⡾⠛⠛⢷⣦⣄⠀
// ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣧⠀⠀⠈⠉⣀⡀⠀ ⠀⠙⢿⡇
// ⠀⠀⠀⠀⠀⠀⢀⣠⣴⡿⠟⠋⠀⠀⢠⣾⠟⠃⠀⠀⠀⢸⣿⡆
// ⠀⠀⠀⢀⣠⣶⡿⠛⠉⠀⠀⠀⠀⠀⣾⡇⠀⠀⠀⠀⠀⢸⣿⠇
// ⢀⣠⣾⠿⠛⠁⠀⠀⠀⠀⠀⠀⠀⢀⣼⣧⣀⠀⠀⠀⢀⣼⠇
// ⠈⠋⠁⠀⠀⠀⠀⠀⠀⠀⠀⢀⣴⡿⠋⠙⠛⠛⠛⠛⠛⠁
// ⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⣾⡿⠋⠀
// ⠀⠀⠀⠀⠀⠀⠀⠀⢾⠿⠋ 
//

6、搜索板子题

和题目名一样，就是搜索板子题， BFS 和 DFS 都能写，这里放的是 BFS 的AC码，主要就是让学会搜索的人都能AC，所以也没涉及任何思维，就纯板子。考虑到这是你们培训讲的最难的算法，估计有好多人还没学，所以归到了困难题。

#include <bits/stdc++.h>
using namespace std;
#define endl "\n"

typedef pair<int, int> pii;

int w, h;
char graph[1001][1001];
bool visited[1001][1001];

int cnt = 0;

void bfs(int startx, int starty) {
    queue<pii> q;
    q.push({startx, starty});
    visited[startx][starty] = true;
    cnt++;

    int dx[] = {-1, 0, 1, 0};
    int dy[] = {0, 1, 0, -1};

    while (!q.empty()) {
        int currentx = q.front().first;
        int currenty = q.front().second;
        q.pop();

        for (int i = 0; i < 4; ++i) {
            int newx = currentx + dx[i];
            int newy = currenty + dy[i];

            if (newx >= 0 && newx < h && newy >= 0 && newy < w && graph[newx][newy] == '.' && !visited[newx][newy]) {
                q.push({newx, newy}); 
                visited[newx][newy] = true;
                cnt++;
            }
        }
    }
}

int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);

    int startx, starty;
    cin >> w >> h;

    for (int i = 0; i < h; ++i) {
        for (int j = 0; j < w; ++j) {
            cin >> graph[i][j];
            if (graph[i][j] == '@') {
                startx = i;
                starty = j;
            }
        }
    }

    bfs(startx, starty);
    cout << cnt << endl;

    return 0;
}

7、数好数字

这题是一个简单数论，虽然难度不高，但由于是数论我们还是把它归为了中等题。

大概就是根据好数的周期性，以210为周期，每个210内的好数数量都一样。

先计算一下 2 到 r 的好数数量，再计算一下 2 到 l 的好数数量，然后一减就是 l 到 r 的好数数量。

注意开long long！！！

#include <iostream>
using namespace std;
#define endl "\n"

const int LCM = 210; // 2*3*5*7=210

// 判断一个数是否不被2、3、5、7中的任何一个整除
bool good(int x) {
    return x % 2 > 0 && x % 3 > 0 && x % 5 > 0 && x % 7 > 0;
}

// 计算[0, x)范围内满足good条件的数字数量
int get_naive(int x) {
    int ans = 0;
    for (int i = 1; i <= x; ++i) {
        if (good(i)) {
            ans++;
        }
    }
    return ans;
}

// 优化计算：利用210是2、3、5、7的最小公倍数，减少重复计算
long long get(long long r) {
    return (r / LCM) *48 + get_naive(r % LCM);
}  

int main() {
    int t;
    cin >> t;

    while (t--) {
        long long l, r;
        cin >> l >> r;
        // 计算[l, r]范围内满足条件的数字数量
        cout << get(r) - get(l-1) << endl;
    }

    return 0;
}

8、什么？你...你竟然是尊贵的传奇王者？

简单数学题，由奇+奇=偶、偶+偶=偶、奇+偶=奇，所以只需统计一下奇偶数量，如果奇偶数量相等，则就能恰好分割，则输出 “ Yes ” ，否则输出 “ No ” 。

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"

int a[205]={};

int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        int cntj=0,cnto=0;
        int n;
        cin>>n;
        for(int i=0;i<2*n;++i){
            cin>>a[i];
            if(a[i]%2==1)
                cntj++;
            else
                cnto++;
        }
        if(cntj==cnto)
            cout<<"Yes"<<endl;
        else
            cout<<"No"<<endl;

    }
    return 0;
}

9、这是什么图形

这是一道小学题，正方形的性质可知对角线相等，那么一半都相等

#include <bits/stdc++.h>
using namespace std;

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    int t;
    cin >> t;
    while (t--) {
        int l, r, d, u;
        cin >> l >> r >> d >> u;
        if (l == r && d == u && l == d) {
            cout << "Yes\n";
        } else {
            cout << "No\n";
        }
    }
    return 0;
}

10、haxin学姐的旅程规划

让我们把陈述中给出的等式变形重新写成 $c{i+1}−b{c{i+1}}=c{i}−b{c{i}}$ 。这意味着我们旅行计划中路径上的所有城市将具有相同的 $i−b_{i}$ 值，即索引值减去对应的美丽值，这个性质可以通过上面那种对题目中的等式进行变形得到，也可以通过画图得知，就自己画两个线段然后就能琢磨出来。

这题用到C++的一个map容器，没学过的学一下，这个容器挺重要的，大概就是能将两个量关联起来。这一题的思路就是先遍历一遍数组b，并用map的第一个参数放 $i−b{i}$ 值，将 $i−b{i}$ 值相同的元素的值累加起来存到第二个参数中，这样就把 $i−b{i}$ 值和与它相对应的美丽值之和关联在一起了，通过第一个参数的值就能直接访问到与之对应的第二个参数的值。此外，把数组从头遍历到尾，就是满足了题目中序列严格递增的要求。最后再遍历一遍map，map中最大的第二个参数值就是答案，即最大美丽值。另外，数据范围上，虽然n和 $b{i}$ 都没超过 int 范围，但是答案有可能将 n 个 $b_{i}$ 相加，这就超过了 int 范围，所以要开long long，map的第二个参数和 ans 都要开 long long。

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"

int b[200050]={};

int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
    int n;
    cin>>n;
    map<int,long long>mapp;
    for(int i=1;i<=n;++i){
        cin>>b[i];
    }
    int x;
    for(int i=1;i<=n;++i){
        x=i-b[i];
        mapp[x]+=b[i];
    }
    long long ans=0;
    for(auto p:mapp){
        if(p.second>ans)
            ans=p.second;
    }
    cout<<ans<<endl;
    return 0;
}

11、挑剔的猫

思路：在开始之前，我们先求出所有元素的绝对值，因为它们的符号并不重要。然后，如果数组的第一个元素等于或小于数组的[n/2]+1最小元素，则答案是可能的。否则，答案就是不可能的

#include<bits/stdc++.h>
using namespace std;

const int N=1e5+10;
int a[N];

int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        int n;scanf("%d",&n);
        for(int i=1;i<=n;i++)
            scanf("%d",&a[i]);
        int f=abs(a[1]);
        int cnt=0;
        for(int i=2;i<=n;i++){
            int z=abs(a[i]);
            if(z<=f)
                cnt++;
        }
        if(cnt+1<=(n/2+1))
            cout<<"YES"<<endl;
        else
            cout<<"NO"<<endl;
    }
    return 0;
}

12、这是啥博弈？

诈骗题，提示里也提醒了，输出获胜者名字的第一个字母，而两个人的第一个字母都是 ’ B ‘ ，所以直接输入n，然后直接输出 ’ B ‘ 就行了。但对于这题来说，也可以不用输入 n ，直接输出 ’ B ‘ ，因为AC的标准就是只看你输出的数据和后台的数据是否能完全吻合，不看输入。不要觉得这种诈骗题很奇怪，这都是我们平常碰到过的，很多比赛都有，比如我们学校前年举办的新生河南省邀请赛里就有一道，如果感兴趣的话，可以看看。

#include<bits/stdc++.h>
using namespace std;
#define endl "\n"

int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
    cout<<'B'<<endl;
    return 0;
}

//
// ⠀⠀⠀             ⠀⢸⣿⣿⣿⠀⣼⣿⣿⣦⡀
// ⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⠀⠀⠀ ⠀⢸⣿⣿⡟⢰⣿⣿⣿⠟⠁
// ⠀⠀⠀⠀⠀⠀⠀⢰⣿⠿⢿⣦⣀⠀⠘⠛⠛⠃⠸⠿⠟⣫⣴⣶⣾⡆
// ⠀⠀⠀⠀⠀⠀⠀⠸⣿⡀⠀⠉⢿⣦⡀⠀⠀⠀⠀⠀⠀ ⠛⠿⠿⣿⠃
// ⠀⠀⠀⠀⠀⠀⠀⠀⠙⢿⣦⠀⠀⠹⣿⣶⡾⠛⠛⢷⣦⣄⠀
// ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⣿⣧⠀⠀⠈⠉⣀⡀⠀ ⠀⠙⢿⡇
// ⠀⠀⠀⠀⠀⠀⢀⣠⣴⡿⠟⠋⠀⠀⢠⣾⠟⠃⠀⠀⠀⢸⣿⡆
// ⠀⠀⠀⢀⣠⣶⡿⠛⠉⠀⠀⠀⠀⠀⣾⡇⠀⠀⠀⠀⠀⢸⣿⠇
// ⢀⣠⣾⠿⠛⠁⠀⠀⠀⠀⠀⠀⠀⢀⣼⣧⣀⠀⠀⠀⢀⣼⠇
// ⠈⠋⠁⠀⠀⠀⠀⠀⠀⠀⠀⢀⣴⡿⠋⠙⠛⠛⠛⠛⠛⠁
// ⠀⠀⠀⠀⠀⠀⠀⠀⠀⣀⣾⡿⠋⠀
// ⠀⠀⠀⠀⠀⠀⠀⠀⢾⠿⠋ 
//